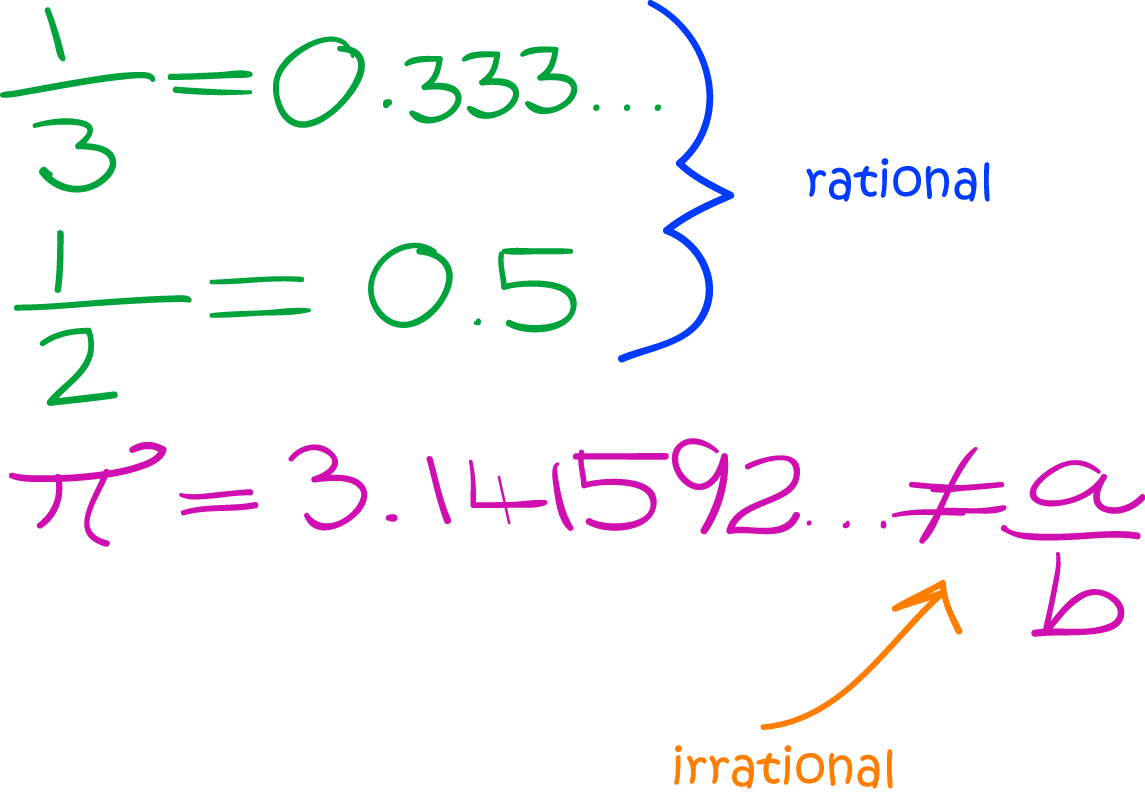An irrational number is a real number that cannot be expressed as a simple fraction of two integers. Irrational numbers contrast with rational numbers, which can be expressed as fractions. The set of all rational numbers is countable, while the set of all irrational numbers is uncountable. This means that there are infinitely many irrational numbers. The most famous example of an irrational number is the square root of 2, which is approximately equal to 1.414.
Irrational numbers play an important role in mathematics. They are used to describe many natural phenomena, such as the growth of plants and the motion of planets. Irrational numbers are also used in cryptography and computer science.
The discovery of irrational numbers was a major turning point in the history of mathematics. It led to the development of new mathematical theories and helped to shape our understanding of the real world.
What is an Irrational Number?
An irrational number is a real number that cannot be expressed as a simple fraction of two integers. Irrational numbers are contrasted with rational numbers, which can be expressed as fractions. The set of all rational numbers is countable, while the set of all irrational numbers is uncountable. This means that there are infinitely many irrational numbers. The most famous example of an irrational number is the square root of 2, which is approximately equal to 1.414.
- Definition: An irrational number is a real number that cannot be expressed as a simple fraction of two integers.
- Example: The square root of 2 is an irrational number.
- Uncountability: The set of all irrational numbers is uncountable.
- Importance: Irrational numbers are used to describe many natural phenomena, such as the growth of plants and the motion of planets.
- History: The discovery of irrational numbers was a major turning point in the history of mathematics.
- Applications: Irrational numbers are used in cryptography and computer science.
Irrational numbers are an important part of mathematics. They are used to describe many natural phenomena, and they have applications in cryptography and computer science. The discovery of irrational numbers was a major turning point in the history of mathematics, and it helped to shape our understanding of the real world.
1. Definition
This definition is important because it provides a clear and concise way to identify irrational numbers. It also helps us to understand why irrational numbers are important in mathematics. Irrational numbers are used to describe many natural phenomena, such as the growth of plants and the motion of planets. They are also used in cryptography and computer science.
For example, the square root of 2 is an irrational number. This means that it cannot be expressed as a simple fraction of two integers. The decimal representation of the square root of 2 is non-terminating and non-repeating. This means that it goes on forever without repeating any pattern.
The discovery of irrational numbers was a major turning point in the history of mathematics. It led to the development of new mathematical theories and helped to shape our understanding of the real world.
2. Example
This example is important because it provides a concrete illustration of an irrational number. The square root of 2 is a number that cannot be expressed as a simple fraction of two integers. This means that it is a non-terminating, non-repeating decimal. The square root of 2 is also an irrational number because it cannot be constructed using a compass and straightedge.
- The square root of 2 is an irrational number because it is non-terminating and non-repeating. This means that it goes on forever without repeating any pattern. For example, the decimal representation of the square root of 2 is 1.41421356237309504880168872420969... This decimal representation never ends and never repeats any pattern.
- The square root of 2 is an irrational number because it cannot be constructed using a compass and straightedge. This means that it is impossible to construct a square with an area equal to 2 using only a compass and straightedge. This was proven by the ancient Greek mathematician Hippasus of Metapontum.
The square root of 2 is just one example of an irrational number. There are infinitely many irrational numbers, and they play an important role in mathematics. Irrational numbers are used to describe many natural phenomena, such as the growth of plants and the motion of planets. They are also used in cryptography and computer science.
3. Uncountability
The uncountability of the set of all irrational numbers is a fundamental property that distinguishes irrational numbers from rational numbers. A set is countable if it is either finite or if it can be put into a one-to-one correspondence with the set of natural numbers. The set of rational numbers is countable because it can be put into a one-to-one correspondence with the set of integers. However, the set of irrational numbers is uncountable. This means that there is no way to list all of the irrational numbers in a sequence.
The uncountability of the set of irrational numbers has important implications for our understanding of the real numbers. It means that there are infinitely many irrational numbers, and that they are not all expressible in terms of simple fractions. This has led to the development of new mathematical theories, such as measure theory and topology, which are used to study the properties of sets of real numbers.
The uncountability of the set of irrational numbers is also important in computer science. For example, it is used in the design of algorithms for finding prime numbers and for solving other mathematical problems.
4. Importance
Irrational numbers are essential for describing many natural phenomena because they represent quantities that cannot be expressed as simple fractions. For example, the growth of plants is often described using irrational numbers, such as the golden ratio. The golden ratio is an irrational number approximately equal to 1.618, and it is found in many natural forms, such as the spirals of seashells and the arrangement of leaves on a stem. Irrational numbers are also used to describe the motion of planets. The orbits of planets are not perfect circles, and they can be described using irrational numbers. For example, the eccentricity of Earth's orbit is an irrational number approximately equal to 0.0167. This means that Earth's orbit is slightly elliptical, rather than perfectly circular.
The importance of irrational numbers in describing natural phenomena cannot be overstated. Without irrational numbers, we would not be able to accurately describe many of the patterns and processes that we observe in the world around us. Irrational numbers are essential for our understanding of the natural world.
In addition to their importance in describing natural phenomena, irrational numbers also have practical applications in many fields, such as engineering, computer science, and finance. For example, irrational numbers are used to design bridges, buildings, and other structures. They are also used to develop algorithms for computer graphics and to model financial markets.
5. History
The discovery of irrational numbers was a major turning point in the history of mathematics because it led to the development of new mathematical theories and helped to shape our understanding of the real world. Before the discovery of irrational numbers, it was believed that all numbers could be expressed as simple fractions of two integers. However, the discovery of irrational numbers showed that this was not the case. Irrational numbers are numbers that cannot be expressed as simple fractions, and they are essential for describing many natural phenomena, such as the growth of plants and the motion of planets.
- New mathematical theories
The discovery of irrational numbers led to the development of new mathematical theories, such as measure theory and topology. These theories are used to study the properties of sets of real numbers, including irrational numbers. Measure theory is used to measure the size of sets of real numbers, and topology is used to study the structure of sets of real numbers.
- Understanding of the real world
The discovery of irrational numbers helped to shape our understanding of the real world. Irrational numbers are essential for describing many natural phenomena, such as the growth of plants and the motion of planets. Without irrational numbers, we would not be able to accurately describe many of the patterns and processes that we observe in the world around us.
- Applications in other fields
Irrational numbers also have applications in other fields, such as engineering, computer science, and finance. For example, irrational numbers are used to design bridges, buildings, and other structures. They are also used to develop algorithms for computer graphics and to model financial markets.
The discovery of irrational numbers was a major turning point in the history of mathematics. It led to the development of new mathematical theories, helped to shape our understanding of the real world, and has applications in many other fields.
6. Applications
Irrational numbers play a significant role in cryptography and computer science due to their unique properties. Their non-terminating and non-repeating nature makes them highly resistant to certain types of attacks.
- Cryptography
In cryptography, irrational numbers are used to generate encryption keys that are difficult to break. Encryption keys are used to protect sensitive information, such as financial data and personal communications. The security of these keys depends on their unpredictability, and irrational numbers provide a high level of unpredictability due to their infinite and non-repeating nature.
- Computer science
In computer science, irrational numbers are used in various applications, including computer graphics and numerical analysis. In computer graphics, irrational numbers are used to create smooth curves and surfaces, as well as to simulate natural phenomena such as turbulence and diffusion. In numerical analysis, irrational numbers are used to solve complex mathematical problems, such as finding the roots of equations and integrating functions.
The use of irrational numbers in cryptography and computer science is a testament to their unique properties and their importance in modern technology.
FAQs about Irrational Numbers
Irrational numbers are real numbers that cannot be expressed as a simple fraction of two integers. They are an important part of mathematics, and they have applications in many fields, such as cryptography and computer science.
Question 1: What is an irrational number?
Answer: An irrational number is a real number that cannot be expressed as a simple fraction of two integers.
Question 2: Why are irrational numbers important?
Answer: Irrational numbers are important because they are used to describe many natural phenomena, such as the growth of plants and the motion of planets. They are also used in cryptography and computer science.
Question 3: What is an example of an irrational number?
Answer: The square root of 2 is an irrational number.
Question 4: How are irrational numbers used in cryptography?
Answer: Irrational numbers are used in cryptography to generate encryption keys that are difficult to break.
Question 5: How are irrational numbers used in computer science?
Answer: Irrational numbers are used in computer science in various applications, such as computer graphics and numerical analysis.
Summary of key takeaways or final thought: Irrational numbers are an important part of mathematics, and they have applications in many fields. They are used to describe many natural phenomena, and they are also used in cryptography and computer science.
Transition to the next article section: To learn more about irrational numbers, please see the following article: Irrational Numbers: A Deeper Dive
Conclusion
Irrational numbers are real numbers that cannot be expressed as a simple fraction of two integers. They are an important part of mathematics, and they have applications in many fields, such as cryptography and computer science.
The discovery of irrational numbers was a major turning point in the history of mathematics. It led to the development of new mathematical theories and helped to shape our understanding of the real world. Irrational numbers are essential for describing many natural phenomena, such as the growth of plants and the motion of planets. They are also used in cryptography and computer science to solve complex problems and protect sensitive information.
You Might Also Like
Hard Pythagorean Theorem Problems: Master The ChallengeUncover Your Destiny: The April 24 Star Sign Revealed
The Ultimate Guide To Taurus-Aries Compatibility: Uncover The Secrets
Ryan LeVert: The Ultimate Guide To His Music And Legacy
Donald Trump's Remarkable Height: Surprising Measurements
Article Recommendations